


Some problems require performance that only massively parallel
computers offer whose programming is still difficult. Works on
functional programming and parallelism can be divided in two
categories: explicit parallel extensions of functional languages ---
where languages are either non-deterministic
[29] or non-functional [2, 10]
--- and parallel implementations with functional semantics
[1] --- where resulting languages do not express
parallel algorithms directly and do not allow the prediction of
execution times. Algorithmic skeleton languages
[7, 30], in which only a finite set of
operations (the skeletons) are parallel, constitute an intermediate
approach. Their functional semantics is explicit but their parallel
operational semantics is implicit. The set of algorithmic skeletons
has to be as complete as possible but it is often dependent on the
domain of application.
The design of parallel programming languages is therefore a tradeoff
between:
-
the possibility of expressing parallel features necessary for
predictable efficiency, but which make programs more difficult to
write, to prove and to port
- the abstraction of such features that are necessary to make
parallel programming easier, but which must not hinder efficiency
and performance prediction.
We are exploring thoroughly the intermediate position of the paradigm
of algorithmic skeletons in order to obtain universal parallel
languages where execution cost can be easily determined from the
source code (in this context, cost means the estimate of parallel
execution time). This last requirement forces the use of explicit
processes corresponding to the parallel machine's processors. Bulk Synchronous Parallel (BSP) computing [27] is a
parallel programming model which uses explicit processes, offers a
high degree of abstraction and yet allows portable and predictable
performance on a wide variety of architectures.
A denotational approach led us to study the expressiveness of
functional parallel languages with explicit processes [16]
but this is not easily applicable to BSP algorithms. An operational
approach has led to a BSP lambda-calculus that is confluent and
universal for BSP algorithms [25], and to a library of
bulk synchronous primitives for the Objective Caml [21]
language which is sufficiently expressive and allows the prediction of
execution times [15].
This framework is a good tradeoff for parallel programming because:
-
we defined a confluent calculus so
-
we can design purely functional parallel languages from it.
Without side-effects, programs are easier to prove, and to re-use
(the semantics is compositional)
- we can choose any evaluation strategy for the language. An
eager language allows good performances.
- this calculus is based on BSP operations, so programs are easy
to port, their costs can be predicted and are also portable because
they are parametrized by the BSP parameters of the target
architecture.
The version 0.1 of our BSMLlib library implements the
BSlambda-calculus primitives using Objective Caml [21]
and BSPlib [17] and its performance follows curves
predicted by the BSP cost model [3]. This environment
is a safe one. Our language is deterministic, is based on a parallel
abstract machine [28] which has been proved correct
w.r.t. the confluent BSlambdap-calculus [22]
using an intermediate semantics [23]. A polymorphic type
system [12] has been designed, for which type inference
is possible. The small number of basic operations allows BSMLlib
to be taught to BSc. students.
The BSPlib library is no longer supported nor updated. Moreover
BSMLlib is used as the basis for the Caraml project which
aims to use Objective Caml for Grid computing with, for example,
applications to parallel databases and molecular simulation. In such
a context, the parallel machine is no longer a homogeneous machine as
prescribe by the BSP model and global synchronisation barriers are too
costly. Thus we will need encapsulated communications between
differents architectures and subset synchronization
[32]. The new version 0.2 of the BSMLlib library
is hence base on MPI [34]. It also has a smaller number of
primitives which are closer to the BSlambda-calculus than the
primitives of the version 0.1. In version 0.1, communication
primitives manipulate parallel vectors of lists and parallel vectors
of hash tables and are less easy to be taught.
The section 1.1 presents the BSP model, section
1.2 explains why processes should be explicit in parallel
programming languages and compares our approach with the SPMD
paradigm. Section 1.3 gives an overview of the core
BSMLlib library.
1.1 The BSP Model
The Bulk Synchronous Parallel (BSP) model
[35, 26, 33] describes: an
abstract parallel computer, a model of execution and a cost model. A
BSP computer has three components: a homogeneous set of
processor-memory pairs, a communication network allowing inter
processor delivery of messages and a global synchronization unit which
executes collective requests for a synchronization barrier. A wide
range of actual architectures can be seen as BSP computers.
The performance of the BSP computer is characterized by three
parameters (expressed as multiples the local processing speed): the
number of processor-memory pairs p ; the time l
required for a global synchronization ; the time g for
collectively delivering a 1-relation (communication phase where every
processor receives/sends at most one word). The network can deliver an
h-relation (communication phase where every processor receives/sends
at most h words) in time g× h. Those parameters can easily
be obtained using benchmarks [17].
A BSP program is executed as a sequence of super-steps, each one
divided into (at most) three successive and logically disjointed phases
(Fig. 1.1):
-
Each processor uses its local data (only) to
perform sequential computations and to request data transfers to/from
other nodes;
- the network delivers the requested data transfers;
- a global synchronization barrier
occurs, making the transferred data available for the next super-step.
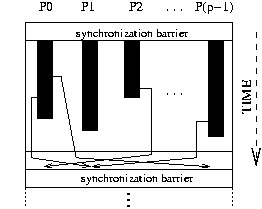
bspstep
Figure 1.1: A BSP super-step
The execution time of a super-step s is, thus, the sum of the maximal
local processing time, of the data delivery time and of the global
synchronization time:
| Time |
(s)= |
|
wi(s) +
|
|
hi(s)× g + l |
The execution time sumsTime(s) of a BSP program composed of
S super-steps is, therefore, a sum of 3 terms:
| W + H× g +
S× l where
|
{
{
{
{
{
{
{
{
{
{
{
{
{
{ |
|
|
In general, W,H and S are functions of p and of the size of data
n, or of more complex parameters like data skew. To minimize
execution time, the BSP algorithm design must jointly minimize the
number S of super-steps, the total volume h with imbalance of
communication and the total volume W with imbalance of local
computation.
Bulk Synchronous Parallelism (and the Coarse-Grained Multicomputer,
CGM, which can be seen as a special case of the BSP model) is used for
a large variety of applications: scientific computing
[5, 19], genetic algorithms [6] and
genetic programming [8], neural networks
[31], parallel databases [4], constraint
solvers [13], etc. It is to notice that ``A
comparison of the proceedings of the eminent conference in the field,
the ACM Symposium on Parallel Algorithms and Architectures, between
the late eighties and the time from the mid nineties to today reveals
a startling change in research focus. Today, the majority of research
in parallel algorithms is within the coarse-grained, BSP style,
domain'' [9].
1.2 Explicit processes and the SPMD programming style
Among researchers interested in declarative parallel programming,
there is a growing interest in execution cost models taking into
account global hardware parameters like the number of processors and
bandwidth. With similar motivations we are designing an extension of
ML called BSML for which the BSP cost model facilitates performance
prediction. Its main advantage in this respect is the use of explicit processes: the map from processors to data is programmed
explicitly and does not have to be recovered by inverting the
semantics of layout directives.
In BMSL, a parallel value is built from an ML
function from processor numbers to local data. A computation
superstep results from the pointwise application of a parallel
functional value to a parallel value. A communication and
synchronization superstep is the application of a communication template
(a parallel value of processor numbers) to a parallel value.
A crucial restriction on the language's constructors is that
parallel values are not nested.
Such nesting would imply either dynamic process
creation or some non-constant dynamic costs for mapping parallel
values to the network of processors, both of which would contradict
our goal of direct-mode BSP programming.
The popular style of SPMD programming in a sequential language
augmented with a communication library has some advantages due to its
explicit processes and explicit messages. In it, the programmer can
write BSP algorithms and control the parameters that define execution
time in the cost model. However, programs written in this style are
far from being pure-functional: they are imperative and even
non-deterministic. There is also an irregular use of the pid
(Processor ID i.e. processor number) variable which is bound outside the source program. Consider for example p static
processes (we refer to processes as processors without
distinction) given an SPMD program E to execute. The meaning of E
is then
[[ E ]]SPMD = [[ E@0 || ... || E@(p-1) ]]CSP
where E@i = E[pid <- i] and [[ E ]]CSP refers to concurrent
semantics defined by the communication library, for example the meaning of
a CSP process [18].
This scheme has two major disadvantages. First, it uses concurrent semantics
to express parallel algorithms, whose purpose is to execute predictably
fast and are deterministic. Secondly,
the pid variable is used without explicit binding. As a
result there is no syntactic support for escaping from a
particular processor's context to make global decisions about the
algorithm. The global parts of the SPMD program are those
which do not depend on any conditional using the pid variable.
This dynamic property is thus given the role of defining
the most elementary aspect of a parallel algorithm, namely
its local vs global parts.
We propose to eliminate both of these problems by using a minimal set
of algorithmic operations having a BSP interpretation. Our parallel
control structure is analogous to the PAR of Occam [20]
but without possibility of nesting. The pid variable is
replaced by a normal argument to a function within a parallel
constructor. The property of being a local expression is then visible
in the syntax and types. The current implementation of BSML is the
BSMLlib library, which is described below.
1.3 Overview of the core BSMLlib library
There is currently no implementation of a full Bulk Synchronous
Parallel ML language but rather a partial implementation: a library
for Objective Caml. The so-called BSMLlib library is based on the
following elements.
It gives access to the BSP parameters of the underling architecture.
In particular, it offers the function bsp_p:unit->int such that
the value of bsp_p() is p, the static number of processes of
the parallel machine. The value of this variable does not change
during execution (for ``flat'' programming, this is not true if a
parallel juxtaposition is added to the language
[24]).
There is also an abstract polymorphic type 'a par which
represents the type of p-wide parallel vectors of objects of type
'a, one per process. The nesting of par types is
prohibited. Our type system enforces this restriction
[11]. This improves on the earlier design DPML/Caml
Flight [14, 10] in which the global parallel control
structure sync had to be prevented dynamically from
nesting.
This is very different from SPMD programming (Single Program Multiple
Data) where the programmer must use a sequential language and a
communication library (like MPI [34]). A parallel program is
then the multiple copies of a sequential program, which exchange messages
using the communication library. In this case, messages and processes
are explicit, but programs may be non deterministic or may contain
deadlocks.
Another drawback of SPMD programming is the use of a variable
containing the processor name (usually called ``pid'' for Process
Identifier) which is bound outside the source program. A SPMD program
is written using this variable. When it is executed, if the parallel
machine contains p processors, p copies of the program are
executed on each processor with the pid variable bound to the number
of the processor on which it is run. Thus parts of the program that
are specific to each processor are those which depend on the pid
variable. On the contrary, parts of the program which make global
decision about the algorithms are those which do not depend on the
pid variable. This dynamic and undecidable property is given the role
of defining the most elementary aspect of a parallel program, namely,
its local vs global parts.
The parallel constructs of BSML operate on parallel vectors. Those
parallel vectors are created by:
mkpar: (int -> 'a) -> 'a par
so
that (mkpar f) stores (f i) on process i for i between
0 and (p-1). We usually write f as fun pid->e to show
that the expression e may be different on each processor. This
expression e is said to be local. The expression (mkpar f) is a parallel object and it is said to be global.
A BSP algorithm is expressed as a combination of asynchronous local
computations (first phase of a super-step) and phases of global
communication (second phase of a super-step) with global
synchronization (third phase of a super-step).
Asynchronous phases are programmed with mkpar and with:
apply: ('a -> 'b) par -> 'a par -> 'b par
apply (mkpar f) (mkpar e) stores (f i) (e i)
on process i. Neither the implementation of BSMLlib, nor its
semantics [23] prescribe a synchronization
barrier between two successive uses of apply.
Readers familiar with BSPlib [33, 17]
will observe that we ignore the
distinction between a communication request and its realization at the
barrier. The communication and synchronization phases are expressed
by:
put:(int->'a option) par -> (int->'a option) par
Consider the expression:
put(mkpar(fun i->fsi))
(*)
To send a value v from process j to process i, the
function fsj at process j must be such as
(fsj i) evaluates to Some v. To send
no value from process j to process i, (fsj i) must evaluate to None.
Expression (*) evaluates to a parallel vector containing a
function fdi of delivered messages on every process. At
process i, (fdi j) evaluates to None if process j sent no message to process i or
evaluates to Some v if process j sent the value v to
the process i.
The full language would also contain a synchronous conditional
operation:
ifat: (bool par) * int * 'a * 'a -> 'a
such that ifat (v,i,v1,v2)
will evaluate to v1 or v2 depending on the value of v at process i. But Objective Caml is an eager language and
this synchronous conditional operation can not be defined as a
function. That is why the core BSMLlib contains the function: at:bool par -> int -> bool to be used only in the construction:
if (at vec pid) then... else... where (vec:bool par) and
(pid:int). if at expresses communication and
synchronization phases.
Global conditional is necessary of express algorithms like :
| Repeat Parallel Iteration Until Max of local errors < epsilon |
Without it, the global control cannot take into account data
computed locally.
For example, one can define get_one such that :
get_one <x0,..., xp-1 > <i0,..., ip-1 >
= <xi0,..., xip-1 >
(* val replicate : 'a -> 'a par *)
let replicate x =
mkpar (fun pid -> x)
(* val apply2 : ('a -> 'b -> 'c) par -> 'a par -> 'b par -> 'c par
let apply2 f x y =
apply (apply f x) y
(* val get_one; 'a par -> int par -> ' a par *)
let get_one datas srcs =
let pids = parfun (fun i->natmod i (bsp_p())) srcs in
let ask = put(parfun (fun i dst->if dst=i then Some() else None) pids)
and replace_by_data =
parfun2 (fun f d dst->match(f dst)with Some() -> Some d|_->None) in
let reply = put(replace_by_data ask datas) in
parfun (fun(Some x)->x) (apply reply pids)
replicate, apply2 and get_one are parts
of the module Bsmlbase.
1.3.2 Remark on nesting
As explained in the introduction, parallel vectors must not be nested.
The programmer is responsible for this absence of nesting. A program
containing e.g. a type int par par will have a unpredictable
behaviour. This kind of nesting is easy to detect. But nesting can be
more difficult to detect, e.g :
let vec1 = mkpar (fun pid -> pid)
and vec2 =
get_one
(replicate 1)
(mkpar (fun pid->if pid=0
then last()
else pid-1)) in
let couple1 = (vec1,1)
and couple2 = (vec2,1) in
mkpar (fun pid -> if pid<(bsp_p())/2
then snd (couple1)
else snd (couple2))
Objective Caml being a strict language, the evaluation of the last
expression would imply the evaluation of vec1 on the first half
of the network and vec2 on the second half of the network. But
a get implies a synchronization barrier and a mkpar implies
no synchronization barrier. So this will lead to mismatched barriers
and the bevahiour of the program will be unpredictable.
In order to avoid such problems, is is sufficient that every
subexpression of a sequential expression (i.e. with no par type)
is also sequential. The only exception is at whose type is bool par -> int -> bool. But at must only be used in a if then else expression and the two branches of the conditional
must be non-sequential expressions.
We have now a polymorphic type system which ensures the absence of
such nesting [12, 11]. This type system will be
included in a full implementation of the BSMLlight language.








